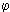= 0.833), stoichiometric ( 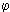= 1.000) and fuel-rich ( 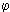= 1.200). Since the fuel feed is constant at all conditions, the change of equivalence ratio involved only the alteration of the amounts of air included in the calculations.
The two different flow regimes can be identified in the drop-tube furnace: Subsequent to fuel injection a conical zone of high recirculation develops, caused not only by the atomisation process, but also by the ignition of the fuel-air mixture, which causes both turbulence and increase of the temperature. This zone can be likened to a continuous stirred tank reactor (CSTR) and it ends at the point of impingement of the fuel-air mixture on the furnace wall. This vertical distance was calculated geometrically to be 100 mm.
After the first 100 mm the ignited, hot, gaseous mixture moves downwards in motion similar to that of a plug flow reactor (PFR). This zone elapsed between 100 mm from the atomiser nozzle and the sampling point, that is 500 mm from the nozzle.
Although clearly separate in the numerical model, there is not a neatly defined boundary between the two zones in the experimental set-up, but they both overlap while the combustion products flow from the CSTR zone into the PFR zone.
The "PSR" code was used in the initial zone of the furnace, whereas the plug flow reactor zone was modelled by means of a "CONP" code. This code was originally written for adiabatic, constant pressure systems. However the drop-tube furnace, although of constant pressure, is not adiabatic. Thus, the "CONP" code was altered so that the experimental temperatures an thus, heat losses were taken into account in the calculations (the modified code is included in "Appendix IV"). Finally, minor modifications were performed to ease the post-processing of the output from both codes.
The "PSR" code was run in ten consecutive batches, each one representing 10 mm of the path of the fuel-gas mixture after exiting the atomiser nozzle. The outlet from a given batch served as the input for the following one. The temperature in each batch was set according to those calculated in chapter V, where the flame temperature was simulated by a second order polynomial with values ranging from that at the point of injection (25 °C) to that at exit of the CSTR zone (100 mm from the atomiser nozzle).
Subsequently, the "CONP" code simulated the plug flow section of the furnace. The outlet composition of the last CSTR batch was used as input to the "CONP" code. This code was run for the equivalent 400 mm, up to a total distance (ie CSTR plus PFR zones) of 500 mm, which was the sampling distance in the experimental work on N-S interactions reported in chapter VII.
The model was run on a PC computer equipped with a Pentium 75 microprocessor and 24 MB RAM. The running time varied according to the number of time step iterations taken by the "PSR" code and the temperature steps given in the input file of the "CONP" code; typical running times for the latter ranged from 15 to 20 minutes.
In this numerical model the fuel composition was simulated by a combination of simple species such as C2H2 and C2H6 for the hydrocarbon content, HCN for the fuel-nitrogen content and H2S for the fuel-sulphur content. Other compounds present in the combustion system, such as H2O in Orimulsion and SO2 in sulphur addition trials were added as separate species.
One of the major limitations of the SANDIA CHEMKIN codes is that only species of up to six elements can be used. This poses restrictions to the form of the species in the fuel feed, which may not be totally representative of the actual ones. The representation of the fuel hydrocarbon content by means of C2H2 and C2H6, although not illustrative of the complex hydrocarbon molecules in heavy distillate fuels, was deemed appropriate in the light of those restrictions. In addition, acetylene and ethane are intermediaries in the combustion of complex hydrocarbons and can be considered in gas phase reactions. HCN is accepted to be the most relevant fuel-N initial species in gas phase in combustion (Hampartsoumian et al. (1991)) . H2S was used as a sulphur-containing compound because sulphur in fuel is normally in its reduced state.
Thus, mole fractions of C2H2, C2H6, HCN and H2S were calculated to match the C, H, N and S contents and the values of the C/H ratio provided in the elemental analyses (see "Appendix II: Analyses of the fuels used in this thesis"). The mole fraction compositions of the different fuels used are shown in the next Table:
| Species | M1 | G1 | Orimulsion |
|---|---|---|---|
| C2H2 | 0.8863 | 0.6721 | 0.5196 |
| C2H6 | 0.0777 | 0.3065 | 0.0696 |
| HCN | 0.0061 | 0.0026 | 0.0066 |
| H2S | 0.0299 | 0.0189 | 0.0210 |
| H2O | 0.0000 | 0.0000 | 0.3832 |
The chemical species considered in the numerical model were composed of five elements, namely C, H, O, N and S. 61 species formed by these elements took part in a mechanism with 264 reactions, which are listed in "Appendix III" along with their reaction rate parameters. The reactions for nitrogen chemistry compiled by Miller and Bowman (Miller and Bowman (1989)) formed the core of the mechanism, which contains reactions for thermal, prompt and fuel-NO formation. In addition, sulphur species were catered for with a set of reactions previously reported by Crosley and Jeffries (Jeffries and Crosley (1986)) and Pfefferle and Churchill (Pfefferle and Churchill (1989)) . These reactions have numbers 234 through to 264.
The reaction mechanism has been validated by Graville (Graville (1993)) and other researchers against a wealth of previously published experimental data. Graville also confirmed the importance of some relevant nitrogen reactions by calculating their sensitivity coefficients, which were in agreement with those reported by other authors (Graville (1993), Pfefferle and Churchill (1989)) .
Another limitation is that CHEMKIN cannot represent processes such as atomisation, droplet combustion and interaction, volatile release and fuel-air mixing. These aspects are of great importance in residual fuels, whereas their relative relevance decreases in more volatile ones such as the distillate fuels used in this thesis. In spite of these limitation, the results from the model showed that these restrictions can be omitted until a more complex model is developed.
Similar to the conditions set in the experimental work reported in chapter VII, three equivalence ratios were simulated, namely fuel-lean (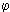 = 0.833), stoichiometric ( 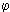= 1.000) and fuel-rich ( 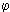= 1.200). Since the fuel feed is constant at all conditions, the change of equivalence ratio involved only the alteration of the amounts of air included in the calculations.
 Previous |  Table of Contents |  Next |