 SO + S reac 40
SO + S reac 40
 SO + S reac 40
SO + S reac 40hydrogen sulphide
O + H2S  OH + SH OH + SH
| reac 41 |
O + SH  SO + H SO + H
| reac 42 |
carbonyl sulphide
 SO + CO reac 43
SO + CO reac 43carbon disulphide
 CS + SO reac 44
CS + SO reac 44SO thus formed is highly reactive and has a lifetime of about a few milliseconds.
 SO2 + M + hv reac 45
SO2 + M + hv reac 45Some authors postulate that the formation of SO2 is actually a process in two steps (Cullis and Mulcahy (1972)) :
O + SO + M  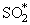 + M + M
| reac 46 |
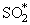  SO2 + hv SO2 + hv
| reac 47 |
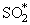 + M + M  SO2 + M SO2 + M
| reac 48 |
SO2 is formed in the flame at rates comparable to H2O, and faster than CO2 (Harris (1990)), its concentration rapidly rising to between 200 and 2,000 ppm.
SO2 may undergo reaction with water in order to form sulphurous acid H2SO3 (Harris (1990)):
 H2SO3 reac 49
H2SO3 reac 49
However, the amount of H2SO3 formed does not represent a problem as its solubility in water is very small at low temperatures and it decreases at higher temperatures (10 % at 20 °C and only 0.58 % by weight at 90 °C). Its solutions are mainly composed of hydrogen sulphite ions (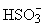 ) and a small percentage of sulphite ions (
) and a small percentage of sulphite ions (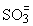 ).
).
In gas turbines the concentration of sulphur trioxide in the exhaust gases is normally between 7 and 11 ppm (Gills (1973)) due to high dilution. However, cases have been reported (Hunter (1982)) of conversion up to 20 %.
Thermodynamic calculations show that the theoretical conversion of SO2 into SO3 at flame temperatures is less than 0.1 %. The direct formation of SO3 by oxygen attack
SO2 + O 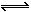 SO3 SO3
| reac 50 |
SO2 + O2 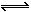 SO3 + O SO3 + O
| reac 51 |
is almost completely displaced to the left at typical combustion temperatures (over 1,000 °C), thus conversion of SO2 into SO3 is very small. In addition, the reaction is extremely slow at such high temperatures, (Hunter (1982)) although it can be catalysed by oxides of W, V, Mo, Cr, Ni and Fe.
However, in practical systems the amount of SO3 produced in the flame is greater than predicted by the equilibrium between SO2 and oxygen at flame temperatures. The reaction is thus assisted by labile species in the flame.
The non-linear dependence of the reaction rate on SO2 concentration suggests that a collisional reaction would be involved with the formation of an activated sulphur trioxide intermediate (Cullis and Mulcahy (1972)), which eventually yields SO3:
O + SO2 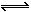 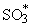
| reac 52 |
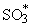 + M + M  SO3 SO3
| reac 53 |
The three-body character of this reaction is demonstrated by its dependence on pressure.
SO3 is also involved in concurrent formation and disappearance reactions (Glassman (1986), Hunter (1982)). Apart from thermal decomposition, SO3 is reduced by:
O + SO3 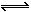 O2 + SO2 O2 + SO2
| reac 54 |
H + SO3 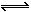 OH + SO2 OH + SO2
| reac 55 |
SO3 + H2 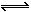 SO2 + H2O SO2 + H2O
| reac 56 |
thus reducing radical concentrations. Simultaneous combustion of CO in the presence of the oxidation of SO2 to SO3 enhances such a process (Hedley (1967)) . Every time one CO molecule is burned one oxygen atom disappears but two of them are formed, thus a surplus of oxygen atoms is created.
The conversion of SO2 into SO3 is affected by several factors (Harris (1990)) :
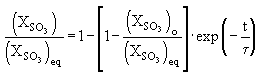
where:
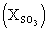 : mole fraction of SO3
: mole fraction of SO3
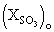 : mole fraction of SO3 initially present, at t = 0
: mole fraction of SO3 initially present, at t = 0
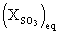 : equilibrium SO3 mole fraction, which is a function of equivalence ratio, pressure and temperature, so that at high temperature its values are low.
: equilibrium SO3 mole fraction, which is a function of equivalence ratio, pressure and temperature, so that at high temperature its values are low.
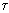 : relaxation time =
: relaxation time = 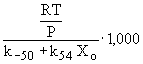
k-50: reverse reaction constant for reaction 50 = 7.41×1020 T-1 exp(-82,689/RT), cm3 mol-1 s-1
k54: reaction constant for reaction 54 = 1.2×1012 exp(-9,500/RT), cm3 mol-1 s-1
XO: O-atom concentration
Typical residence times in the dilution zone of a gas turbine combustor are in a range from 1 to 100 ms, and measured values of SO3 range from 2 to 8 % of SOX. These values are similar to those calculated by Hunter's model: For relaxation times between 0.3 and 30 ms equilibrium levels of SO3 range from 2 to 8 % of SOX.
Hedley (Hedley (1967)) performed experiments in a monodimensional boiler and found SO3 concentrations in the flame stage to be much higher than theoretical equilibrium values, decaying afterwards to remain lower than those of theoretical equilibrium.
By assuming that an activated SO3 molecule was formed and decomposed by means of
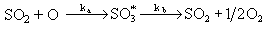
a maximum concentration of sulphur trioxide was calculated
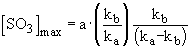
which is reached at a time
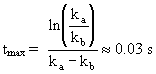
However this model is only applicable to isothermal conditions as the rate coefficients are temperature dependent.
Formation of SO3 in combustion systems is undesirable because it forms H2SO4 with H2O:
SO3 + H2O  H2SO4 H2SO4
| reac 58 |
H2SO4 + 2 H2O  2 H3O+ + 2 H3O+ + 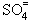
| reac 59 |
As the combustion gases exit from the combustor their temperature decreases and H2SO4 is formed which eventually condenses at a suitable temperature, the acid dew point. Sulphuric acid causes corrosion on Ni-based alloys used in boilers and in other equipment located downstream from the combustor, such as that in combined systems.
The acid dew point is defined (Harris (1990)) as the highest temperature at which H2SO4 vapour (SO3 + H2O) is in equilibrium with H2SO4 liquid at a given pressure. Typical values are around 130 °C, and they increase (ie condensation is more easily attained) as the amounts of SO3 and moisture in the exhaust increase. Also dust and solid particulates in the gas exhaust (Cunningham (1978)) can increase the acid dewpoint.
An expression for calculation of acid dew points was given by Verhoff and Banchero (Harris (1990)):
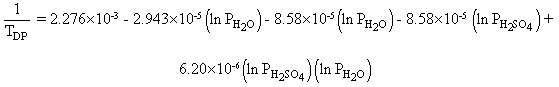
where
TDP: dew point
P: partial pressure
SO3 is a well-known promoter of carbon formation when added in small amounts (approximately 0.1 %) (Cullis and Mulcahy (1972)). However, if added in larger proportions (several percent) along with hydrogen sulphide it helps to decrease carbon formation.
If carbonaceous deposits are present, sulphuric acid may condense in corrosive particles forming acid smuts, especially below 1 % excess oxygen (Cunningham (1978)) where particulate emissions are high. A threshold of 3 ppm SO3 has been found for the formation of acid smuts. Additives like ammonia, dolomite (CO3CaMg) and oxides (MgO), hydroxides and carbonates of magnesium have been used to neutralise H2SO4, as emissions of Mg or MgSO4 have little environmental effects.
Experimental trials with sorbents like dolomite, hydrated lime and pressure hydrated dolomite lime for sulphur control were made by Cowell et al. (Cowel et al. (1992)). The amount of reduction achieved at a Ca/S ratio of 3 ranged from 55 % for dolomite, 82 % with pressure hydrated dolomite and 90 % with hydrated dolomite. Dolomite is economically most favoured among the three.
 Previous |  Table of Contents |  Next |